Основные понятия
Делители и кратные
Делителем натурального числа a называют натуральное число, на которое a делится без остатка.
Наибольшее натуральное число, на которое делятся без остатка числа a и b, называют наибольшим общим делителем (НОД) этих чисел.
Для того чтобы найти наибольший общий делитель нескольких чисел, нужно:
- Разложить их на простые множители.
- Из множителей, входящих в разложение одного из этих чисел, вычеркнуть те, которые не входят в разложение других чисел.
- Найти произведение оставшихся множителей.
Если наибольший общий делитель двух чисел равен 1, то такие числа называются взаимно простыми. Например, числа 13 и 15 – взаимно простые.
Натуральное число называется простым, если оно имеет только два делителя: единицу и самого себя. Если же число имеет больше двух делителей, то оно называется составным. Исключением из этого правила является число 1, оно не является ни простым, ни составным, так как вообще имеет только один делитель.
Кратным натуральному числу а называют натуральное число, которое делится на а без остатка. Любое натуральное число имеет бесконечно много кратных.
Наименьшим общим кратным (НОК) натуральных чисел a и b называют наименьшее натуральное число, которое кратно и a, и b.
Чтобы найти наименьшее общее кратное нескольких чисел, надо:
- Разложить их на простые множители.
- Выделить множители, входящие в разложение одного из чисел.
- Добавить к ним недостающие множители из разложения остальных чисел.
- Найти произведение получившихся чисел.
В серии интерактивных уроков и тренажеров «Обыкновенные дроби» представлены:
- Делители и кратные. Разложение на простые множители.
- Наибольший общий делитель. Взаимно простые числа. Наименьшее общее кратное.
Обыкновенные (или простые) дроби
Запись вида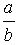 
называется обыкновенной (или простой) дробью. Число a при этом называется числителем, а b – знаменателем.
Дробь, в которой числитель меньше знаменателя, называют правильной дробью.
Дробь, в которой числитель больше знаменателя или равен ему, называют неправильной дробью.
Чтобы из неправильной дроби выделить целую часть, надо:
- разделить с остатком числитель на знаменатель;
- неполное частное будет целой частью
- остаток (если он есть) дает числитель, а делитель — знаменатель дробной части.
Запись числа, содержащую целую и дробную части, называют смешанной. Смешанное число можно представить и в виде неправильной дроби.
Чтобы представить смешанное число в виде неправильной дроби, нужно:
- умножить его целую часть на знаменатель дробной части;
- к полученному произведению прибавить числитель дробной части;
- записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.
Основное свойство дроби: если числитель и знаменатель дроби одновременно умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Правило сокращения дробей: деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби.
В серии интерактивных уроков и тренажеров «Обыкновенные дроби» представлены:
- Основное свойство дроби и правило сокращения дробей.
- Приведение дробей к общему знаменателю. Сравнение дробей.
Сложение и вычитание обыкновенных (простых) дробей
При сложении или вычитании дробей с одинаковыми знаменателями числители соответственно складывают или вычитают, а знаменатель оставляют тот же.
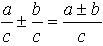
Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем. При приведении дроби к новому знаменателю ее числитель и знаменатель умножают на дополнительный множитель.
Чтобы сравнить, сложить или вычесть дроби с разными знаменателями, надо сначала привести данные дроби к общему знаменателю, а потом сравнить, сложить или вычесть их.
В общем виде сложение и вычитание дробей выглядит так:
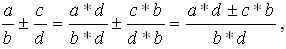
хотя часто удобнее в качестве общего знаменателя брать не простое произведение знаменателей, а наименьшее общее кратное знаменателей данных дробей.
В серии интерактивных уроков и тренажеров «Обыкновенные дроби» представлены:
- Сложение и вычитание дробей с разными знаменателями.
- Смешанные числа. Сложение и вычитание смешанных чисел
Умножение и деление обыкновенных (простых) дробей
Произведение обыкновенных дробей – это дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей данных дробей
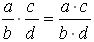
Числа, произведение которых равно 1, называются взаимно обратными.
Чтобы разделить число на дробь, надо умножить эта число на дробь, обратную делителю
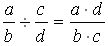
В серии интерактивных уроков и тренажеров «Обыкновенные дроби» представлены: